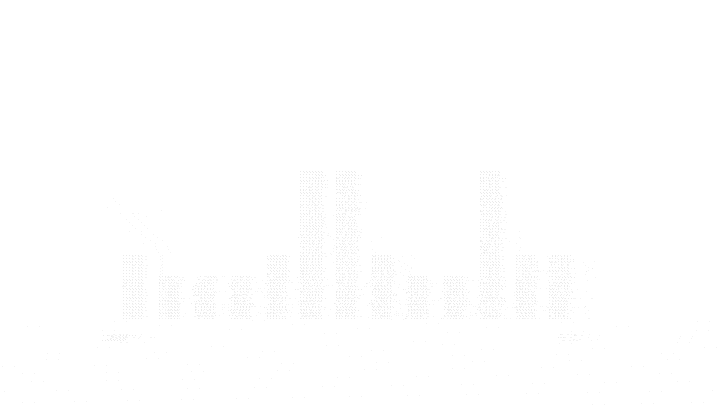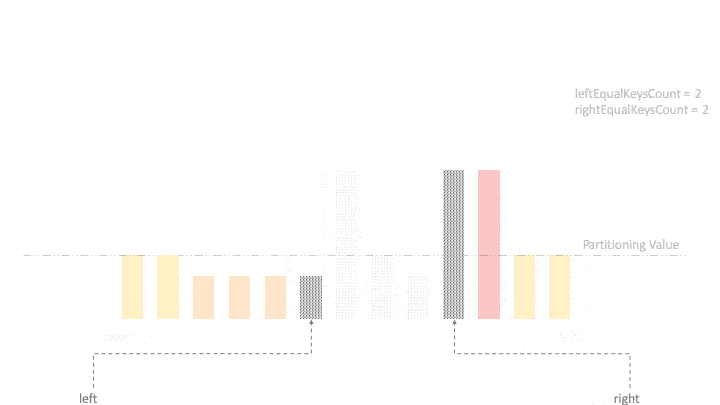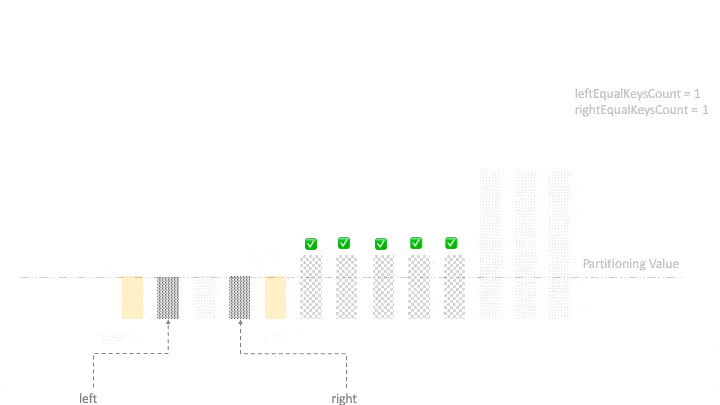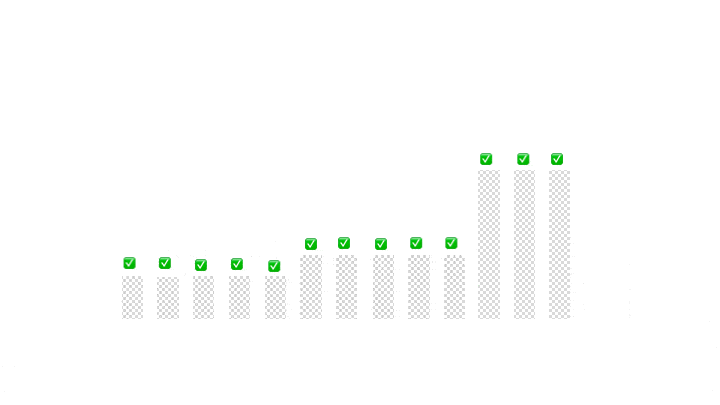1. 概述
算法的运行时复杂性通常取决于输入的性质。
在本教程中,我们将看到快速排序算法的简单实现对于重复元素的性能为何不佳。
此外,我们将学习一些快速排序变体,以便对具有高密度重复键的输入进行有效分区和排序。
2. 简单快速排序
快速排序是一种基于分而治之范式的高效排序算法,从功能上讲,它对输入数组进行就地操作,并通过简单的比较和交换操作重新排列元素。
2.1 单枢轴分区
快速排序算法的一个简单实现很大程度上依赖于单枢轴分区过程,换句话说,分区将数组A = [ap, ap+1, ap+2,…,ar]分为两部分A[p..q]和A[q+1..r],使得:
- 第一个分区中的所有元素A[p..q]都小于或等于枢轴值A[q]
- 第二个分区中的所有元素A[q+1..r]都大于或等于枢轴值A[q]

之后,这两个分区将被视为独立的输入数组,并输入到快速排序算法中,让我们看看Lomuto的快速排序的实际效果:
2.2 重复元素的性能
假设我们有一个数组A = [4,4,4,4,4,4,4],其中所有元素都相等。
使用单枢轴分区方案对此数组进行分区后,我们将得到两个分区,第一个分区将为空,而第二个分区将包含N-1个元素。此外,每次后续调用分区过程都会将输入大小仅减少1。让我们看看它是如何工作的:
由于分区过程具有线性时间复杂度,因此在这种情况下,总时间复杂度是二次方的。对于我们的输入数组来说,这是最坏的情况。
3. 三向分区
为了高效地对包含大量重复键的数组进行排序,我们可以选择更负责任地处理相同的键,这样做的目的是,在第一次遇到它们时就将它们放置在正确的位置。因此,我们寻找数组的三个分区状态:
- 最左边的分区包含严格小于分区键的元素
- 中间分区包含所有与分区键相等的元素
- 最右边的分区包含所有严格大于分区键的元素

我们现在将深入探讨可用于实现三向分区的几种方法。
4. Dijkstra方法
Dijkstra方法是进行三向分区的有效方法,为了理解这一点,我们来研究一个经典的编程问题。
4.1 荷兰国旗问题
受到荷兰三色旗的启发,Edsger Dijkstra提出了一个称为荷兰国旗问题(DNF)的编程问题。
简而言之,这是一个重新排列问题,给定三种颜色的球,随机排列成一条线,要求我们将相同颜色的球组合在一起。此外,重新排列必须确保组遵循正确的顺序。
有趣的是,DNF问题与具有重复元素的数组的三向分区有着惊人的相似之处。
我们可以根据给定的键将数组的所有数字分为三组:
- 红色组包含所有严格小于键的元素
- 白色组包含所有等于键的元素
- 蓝色组包含所有严格大于键的元素

4.2 算法
解决DNF问题的方法之一是选择第一个元素作为分区键,然后从左到右扫描数组。检查每个元素后,将其移动到相应的组,即Lesser、Equal和Greater。
为了跟踪分区进度,我们需要三个指针的帮助,即lt、current和gt。在任何时间点,lt左侧的元素将严格小于分区键,而gt右侧的元素将严格大于键。
此外,我们将使用current指针进行扫描,这意味着current指针和gt指针之间的所有元素都尚待探索:

首先,我们可以将lt和current指针设置在数组的最开始处,将gt指针设置在数组的最末尾:

对于通过current指针读取的每个元素,我们将其与分区键进行比较,并采取以下三种复合操作之一:
- 如果input[current] < key,则我们交换input[current]和input[lt],并增加current和lt指针
- 如果input[current] == key,则我们增加current指针
- 如果input[current] > key,则我们交换input[current]和input[gt]并减少gt
最终,当current指针和gt指针相交时,我们将停止。这样,未探索区域的大小将减少到0,并且只剩下三个必需的分区。
最后,让我们看看该算法如何对具有重复元素的输入数组起作用:
4.3 实现
首先,让我们编写一个名为compare()的实用程序来对两个数字进行三向比较:
public static int compare(int num1, int num2) {
if (num1 > num2)
return 1;
else if (num1 < num2)
return -1;
else
return 0;
}
接下来,让我们添加一个名为swap()的方法来交换同一数组的两个索引处的元素:
public static void swap(int[] array, int position1, int position2) {
if (position1 != position2) {
int temp = array[position1];
array[position1] = array[position2];
array[position2] = temp;
}
}
为了唯一地标识数组中的分区,我们需要其左边界和右边界索引。因此,让我们继续创建一个Partition类:
public class Partition {
private int left;
private int right;
}
现在,我们准备编写三向分区partition()方法:
public static Partition partition(int[] input, int begin, int end) {
int lt = begin, current = begin, gt = end;
int partitioningValue = input[begin];
while (current <= gt) {
int compareCurrent = compare(input[current], partitioningValue);
switch (compareCurrent) {
case -1:
swap(input, current++, lt++);
break;
case 0:
current++;
break;
case 1:
swap(input, current, gt--);
break;
}
}
return new Partition(lt, gt);
}
最后,让我们编写一个quicksort()方法,利用我们的三向分区方案对左右分区进行递归排序:
public static void quicksort(int[] input, int begin, int end) {
if (end <= begin)
return;
Partition middlePartition = partition(input, begin, end);
quicksort(input, begin, middlePartition.getLeft() - 1);
quicksort(input, middlePartition.getRight() + 1, end);
}
5. 本特利-麦克罗伊方法
Jon Bentley和Douglas McIlroy共同编写了快速排序算法的优化版本,让我们理解并在Java中实现此变体:
5.1 分区方案
该算法的关键在于基于迭代的划分方案,一开始,整个数字数组对我们来说都是一个未探索的领域:

然后,我们开始从左到右探索数组的元素,每当我们进入或退出探索循环时,我们都可以将数组视为由5个区域组成:
- 在最两端,存在具有等于分区值元素的区域
- 未探索区域停留在中心,其大小随着每次迭代不断缩小
- 未探索区域的左侧包含所有小于分区值的元素
- 未探索区域的右侧是大于分区值的元素

最终,当没有元素可供探索时,我们的探索循环就会终止。在这个阶段,未探索区域的大小实际上为0,我们只剩下4个区域:

接下来,我们将中心两个相等区域的所有元素移动,使得中心只有一个相等区域,由左侧的较小区域和右侧的较大区域包围。为此,首先,我们将左侧相等区域中的元素与较小区域右端的元素交换。同样,将右侧相等区域中的元素与较大区域左端的元素交换。

最后,我们将只剩下3个分区,并且我们可以进一步使用相同的方法来划分较小的区域和较大的区域。
5.2 实现
在三向快速排序的递归实现中,我们需要对具有不同上下限的子数组调用分区过程。因此,partition()方法必须接收3个输入,即数组及其左边界和右边界。
public static Partition partition(int input[], int begin, int end){
// returns partition window
}
为了简单起见,我们可以选择分区值作为数组的最后一个元素。另外,我们定义两个变量left = begin和right = end来向内探索数组。
此外,我们还需要跟踪最左边和最右边相等元素的数量。因此,让我们初始化leftEqualKeysCount = 0和rightEqualKeysCount = 0,现在我们就可以探索和分区数组了。
首先,我们从两个方向开始移动,找到一个反转点,使得左侧元素不小于分割值,并且右侧元素不大于分割值。然后,除非左右两个指针相互交叉,否则我们交换这两个元素。
在每次迭代中,我们将等于partitioningValue的元素移向两端,并增加相应的计数器:
while (true) {
while (input[left] < partitioningValue) left++;
while (input[right] > partitioningValue) {
if (right == begin)
break;
right--;
}
if (left == right && input[left] == partitioningValue) {
swap(input, begin + leftEqualKeysCount, left);
leftEqualKeysCount++;
left++;
}
if (left >= right) {
break;
}
swap(input, left, right);
if (input[left] == partitioningValue) {
swap(input, begin + leftEqualKeysCount, left);
leftEqualKeysCount++;
}
if (input[right] == partitioningValue) {
swap(input, right, end - rightEqualKeysCount);
rightEqualKeysCount++;
}
left++; right--;
}
在下一个阶段,我们需要将所有相等的元素从两端移到中心。退出循环后,左指针将指向一个值不小于partitioningValue的元素。利用这个事实,我们开始将相等的元素从两端移向中心:
right = left - 1;
for (int k = begin; k < begin + leftEqualKeysCount; k++, right--) {
if (right >= begin + leftEqualKeysCount)
swap(input, k, right);
}
for (int k = end; k > end - rightEqualKeysCount; k--, left++) {
if (left <= end - rightEqualKeysCount)
swap(input, left, k);
}
在最后阶段,我们可以返回中间分区的边界:
return new Partition(right + 1, left - 1);
最后,让我们看一下示例输入上的实现演示:
6. 算法分析
通常,快速排序算法的平均时间复杂度为O(n * log(n)),最坏情况时间复杂度为(n2)。当重复键密度较高时,使用简单的快速排序实现几乎总是会得到最坏的性能。
但是,当我们使用快速排序的三向分区变体(例如DNF分区或Bentley分区)时,我们能够避免重复键带来的负面影响。此外,随着重复键的密度增加,我们算法的性能也会提升。因此,当所有键都相等时,我们会获得最佳性能,并且能够在线性时间内获得包含所有相等键的单个分区。
然而,我们必须注意,当我们从简单的单枢轴分区切换到三向分区方案时,我们本质上增加了开销。
对于基于DNF的方法,开销与重复键的密度无关。因此,如果我们对一个包含所有唯一键的数组使用DNF分区,那么与以最佳方式选择枢轴的简单实现相比,性能会很差。
但是,Bentley-McIlroy的方法很巧妙,因为从两个极端移动相同键的开销取决于它们的数量。因此,即使我们将此算法应用于所有键都唯一的数组,我们也能获得相当不错的性能。
综上所述,单枢轴分区和三向分区算法的最坏时间复杂度均为O(nlog(n))。然而,真正的优势在最佳情况下才显现出来,其中我们看到时间复杂度从单枢轴分区的O(nlog(n))变为三向分区的O(n)。
7. 总结
在本教程中,我们了解了当输入具有大量重复元素时,快速排序算法的简单实现所带来的性能问题。
为了解决这个问题,我们学习了不同的三向分区方案以及如何用Java实现它们。
Post Directory