最佳开源混合整数优化求解器

1. 简介

在本教程中，我们将测试一些用于混合整数规划的开源求解器。

2. 混合整数求解器的优势

在混合整数规划(MIP)中，我们优化至少包含一个整数参数的目标函数，例如：

(1)

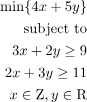
解决混合整数规划(MIP)问题可能非常困难，我们使用专门的求解器来寻找其最优解，现成的求解器具有以下优势：

• MIP求解器适用于解决许多领域的问题，因为许多现实世界的问题都可以建模为MIP问题
• MIP求解器旨在寻找最优解决方案
• 一些MIP求解器具有可扩展性，这意味着它们能够有效处理具有许多决策变量和约束的大规模优化问题
• MIP求解器非常强大，它们能够处理各种类型的问题
• MIP求解器可以与其他工具集成
• MIP求解器可用于各种应用，例如调度、物流、金融、工程等
• MIP求解器可以清晰地理解不同变量之间的权衡，从而做出更好的决策

使用现成的求解器意味着我们无需从头编写代码，从而节省时间。然而，市面上有太多求解器，很难选择，甚至很难确定哪个是最佳的。

3. 我们将测试哪些求解器以及如何测试？

我们重点介绍三种常用的免费开源MIO求解器：

• GLPK(GNU线性规划工具包)能够解决大规模线性、整数、混合整数及相关问题，GLPK使用单纯形法解决线性问题，使用分支定界法处理整数优化问题。
• COIN-OR(运筹学计算基础设施)是一款C++软件，提供一套用于运筹学的高性能工具，其COIN-OR CBC工具可解决混合整数问题。
• PuLP(Python线性规划)包含多个MIO求解器，PuLP用Python编写，使用分支定界算法来优化目标函数。

3.1 性能指标

我们将在问题实例的基准实例上评估每个求解器，每个求解器在每个实例上运行十次。在此过程中，我们将记录最优性差距和求解时间，前者是找到的值与最优值之间的相对差异：

(2)

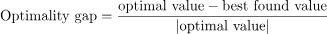
我们将最优性差距计算为已知最佳可行解(或当前解)的目标值与最优目标值(即最佳边界)之间的差值，求解时间是指求解器生成输出所需的时间。

为了解释统计波动和随机性，我们将使用中位数差距及其中位数偏差来比较求解器，因为中位数对异常值的敏感度低于均值。

3.2 基准测试实例

我们使用了以下标准基准实例：

• bnatt400：3600变量和5614约束
• bnatt500：4500变量和7029约束
• neos-631710：167056变量和169576约束
• neos5：63变量和63约束

此外，我们在改变问题规模的同时，对方程(1)上的求解器进行了评估。

我们使用了Python中每个求解器的默认设置。

3.3 需要改变问题规模

评估不同问题规模的MIP求解器有几个目的，包括：

• 研究优化问题的复杂性特征和每个求解器的行为
• 比较MIP求解器在不同问题规模上的性能，可以对不同的求解器进行基准测试
• 它有助于分析求解器在不同问题规模下的计算时间和效率方面的性能
• 它使我们能够评估求解器的可扩展性

4. 比较

我们来检查一下结果。

4.1 求解器在问题规模上的表现

我们在方程(1)中添加了以下形式的通用线性约束：

(3)

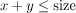
其中size是问题的大小，因为增加它会使搜索空间变大。

随着问题规模的增加，每个求解器的求解时间都呈现出非单调性。COIN-OR CBC和 PuLP的求解时间在规模达到50左右时都急剧增加，之后它们的求解时间变化范围大致相同：

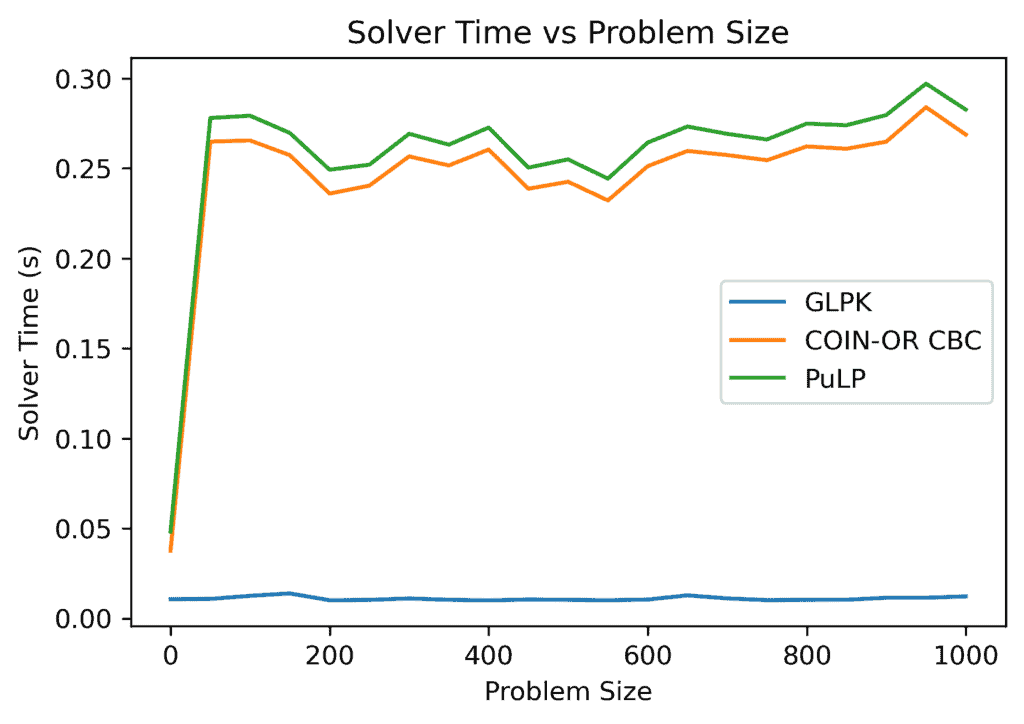
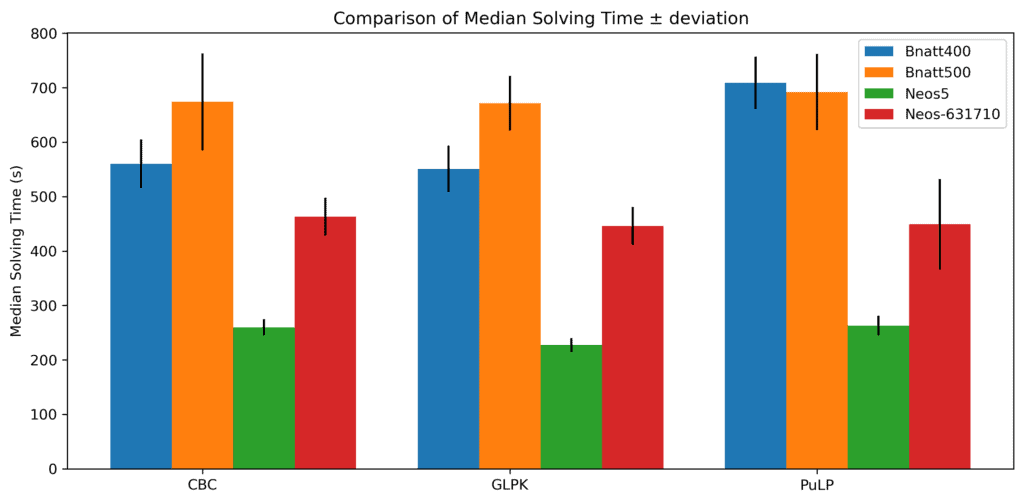
GLPK表现出稳定的行为，偏差约为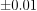秒，也是最快的。COIN-OR CBC和PuLP比GLPK慢，且性能相当。

4.2 基准测试实例上的性能

所有求解器在所有运行中都找到了最优解决方案。

说到时间，每个求解器的时间因实例而异：

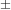中位时间(中位绝对偏差)似乎没有显著差异。

然而，我们可以看到，在bnatt500和neos-631710的案例中，它们的偏差有所不同。PuLP在后者上表现出更大的时间变异性，而在前者上，其变异性与CBC大致相同。一般来说，如果一组求解器的中位求解时间相似，我们会优先选择时间变异最小的那个求解器。

5. 选择最佳求解器

让我们总结一下结果：

标准	COIN-OR CBC(s)	GLPK(s)	PuLP(s)
时间与问题规模	–	✓	–
中位时间	✓	✓	✓
中位数差距	✓	✓	✓

总体而言，GLPK在我们的自定义示例上，在求解时间方面优于其他求解器。在四个基准测试实例上，这些求解器的整体性能大致相同。

但是，使用不同的基准或不同的优化公式可能会导致其他结果。

6. 总结

本文介绍了一些开源混合整数优化求解器，这些求解器凭借其准确性和可扩展性，适用于解决许多领域的问题。我们比较了三种开源求解器：GLPK、COIN-OR CBC和PuLP。虽然GLPK在我们的自定义示例中速度最快，但并没有明显的优胜者。